5091. Explosive
containers
All containers in
the world fall into two categories – with TNT and without.
Only a fool would
place a TNT box on top of another TNT box. Since you’re clearly not one of them
(right?), you know very well that TNT explodes, especially if another TNT box
is placed on top of it.
You find yourself
in a room filled with a vast number of boxes of both types. Suddenly, a lift
emerges from a hatch in the floor. Unfortunately, it is malfunctioning. It has
decided to build a tower of n boxes. To assess your chances of survival,
you need to calculate the number of possible configurations in which nothing
explodes.
By the way, think
about it: what is a rational person like you doing in a room full of TNT?
Input. One integer n (1 ≤ n < 45).
Output. Print the number of safe ways to build the
tower.
|
Sample
input 1 |
Sample
output 1 |
|
1 |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
2 |
3 |
SOLUTION
Fibonacci numbers
Algorithm analysis
Each empty box
is represented by 0, and each TNT box by 1. The task is to determine the number
of strings of length n, consisting of 0s and 1s, such that no two 1s are
adjacent.
The answer to
the problem will be the Fibonacci number f(n):
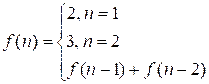
Example
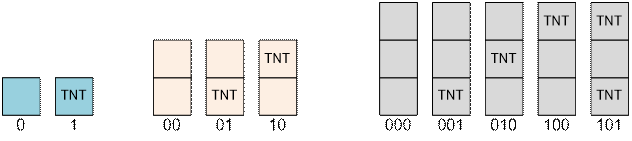
Consider all possible
towers of heights n = 1, n = 2, n = 3. Each corresponds
to a sequence of 0s and 1s. There are:
·
two towers of height 1: “0”, “1”;
·
three towers of height 2: “00”, “01”, “10”;
·
five towers of height 3: “000”, “001”, “010”, “100”, “101”;
Algorithm implementation
Declare an array.
#define MAX 45
int fib[MAX];
Fill the elements of the fib array with Fibonacci numbers according
to the recurrence formula.
fib[1] = 2; fib[2] = 3;
for (int i = 3; i < MAX; i++)
fib[i] = fib[i - 1] + fib[i - 2];
Read the input value of n and print the answer.
scanf("%d", &n);
printf("%d\n", fib[n]);
Algorithm implementation – memoization
Declare an array.
#define MAX 45
int fib[MAX];
The function f computes the n-th Fibonacci
number.
int f(int n)
{
if (n == 1) return 2;
if (n == 2) return 3;
if (fib[n] != -1) return fib[n];
return fib[n] = f(n - 1) + f(n - 2);
}
The main part of the program. Read the input value of n and print
the result.
scanf("%d", &n);
memset(fib, -1, sizeof(fib));
printf("%d\n", f(n));
Java implementation
import java.util.*;
public class Main
{
static int fib[] = new int[45];
static int f(int n)
{
if (n ==
1) return 2;
if (n ==
2) return 3;
if (fib[n] !=
-1) return fib[n];
return fib[n] = f(n-1) +
f(n - 2);
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
Arrays.fill(fib,
-1);
System.out.println(f(n));
con.close();
}
}
Python implementation
– list
Fill the elements of the list lst with Fibonacci numbers according
to the recurrence formula.
lst = [0, 2, 3]
for i in range(3, 45):
lst.append(lst[i - 2] + lst[i - 1])
Read the input value of n and print the result.
n = int(input())
print(lst[n])
Python implementation – memoization
The function fib computes the n-th Fibonacci
number.
def fib(n):
if dp[n] != -1:
return dp[n]
dp[n] = fib(n - 1) + fib(n - 2)
return dp[n]
The main part of the program. Read the input value of n.
n = int(input())
The list dp will store
Fibonacci numbers. Initialize its initial values.
dp = (n + 2) * [-1]
dp[1] = 2
dp[2] = 3
Compute and print the answer.
print(fib(n))